Курсовая работа по обработке изображений

Настоящие методические указания предназначены, прежде всего, для студентов моей специальности 230101 «Вычислительные машины, комплексы, системы и сети», которые хотели бы успешно выполнить курсовую работу по дисциплине с громким названием «Обработка изображений, распознавание образов и мультимедиа». Также они могут быть полезны для студентов и других специальностей и вообще всех интересующихся обработкой изображений и распознаванием текста.

• Задание на курсовую работу


• Документный интерфейс
• Открытие изображения
• Работа с изображением и его отображение
• Работа с точками и цветами
• Яркость точки и гистограммы изображения
• Изменения яркости и контрастности
• Изменение цветности (бинаризация, оттенки серого, негатив)
• Наложение шума и фильтры шумоподавления (сглаживания)
• Методы выделения границ
• Распознавание текста
• Непрерывное преобразование Фурье
• Дискретное преобразование Фурье
• Преобразование Уолша-Адамара


• Источники информации

Непрерывное преобразование Фурье

Ряд вида

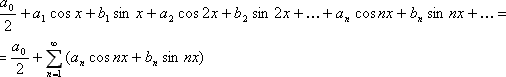
где a₀, a_n, b_n (n є N) – коэффициенты ряда, называется рядом Фурье, или тригонометрическим рядом; возможно искусственное усложнение записи ряда с целью упрощения инженерных расчётов. Ряд Фурье используется для разложения непрерывных функций с целью дискретизации.

Известны формулы Эйлера – Фурье для вычисления коэффициентов ряда Фурье:

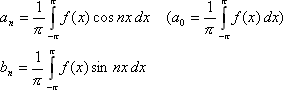
Эти формулы имеют место, если тригонометрический ряд для всех значений x сходится к функции f(x) (предполагается, что эта функция периодическая, с периодом 2π), и для этой функции существует интеграл

Функция f(x) может быть разрывной; при этом указанный интеграл становится несобственным. Непериодические функции, определённые в промежутке (-π; π) тоже можно разлагать в ряд Фурье, но со следующей оговоркой: за пределами указанного промежутка и на его концах ряд Фурье может иметь сумму, отличную от соответствующего значения самой функции.

Теорема. Пусть функция непрерывна на промежутке (-π; π) и либо не имеет здесь разрывов, либо имеет их конечное число. Тогда для этой функции ряд Фурье сходится всюду; сумма его равна значению функции f(x) для всякого значения x є (-π; π), на обоих же концах промежутка сумма ряда равна [f(-π)+f(π)]/2.

Интегралы

для чётной функции равны между собой, а для нечётной – разнятся знаками, поэтому имеем:

соответственно.

Ряд Фурье для чётной функции не содержит синусов, а его коэффициенты равны:

для нечётной функции – не содержит косинусов и имеет коэффициенты:

Практическая реализация

Очевидно, что для работы с произвольными функциями необходимо реализовать универсальную функцию численного интегрирования.

Непрерывное преобразование Фурье выполняется над фиксированным сигналом, не зависящим от загруженного в программу изображения. Этот сигнал описывается функцией вида:

function Signal (X: Real): Real;
  begin
    if Abs (X) > 1 then X := X – 2 * Round (X / 2);
    if X < – 0.4 then Result := 0.25;
    if (X >= – 0.4) and (X < 0.4) then Result := 0.5;
    if (X >= 0.4) and (X < 0.8) then Result := 0.75;
    if X >= 0.8 then Result := 0.25;
  end;

Его интегрирование можно осуществлять численным методом трапеций:

function Integral (F: TFunction; A, B, H: Real): Real;
  var Square, X: Real;
  begin
    Square := 0;
    X := A;
    while X < B – H do
      begin
        Square := Square + 0.5 * (F (X) + F (X + H)) * H;
        X := X + H;
      end;
    Result := Square;
  end;